简介
菲涅耳衍射是基于惠更斯-菲涅尔原理,波前上的每一点都可看作是一个次级子波源,他们发出的子波在空间相遇时会发生干涉叠加,从而在观察屏上形成衍射图样。但是衍射积分很难有解析解,所以对给定的衍射屏,一般采用数值求解。
菲涅耳衍射
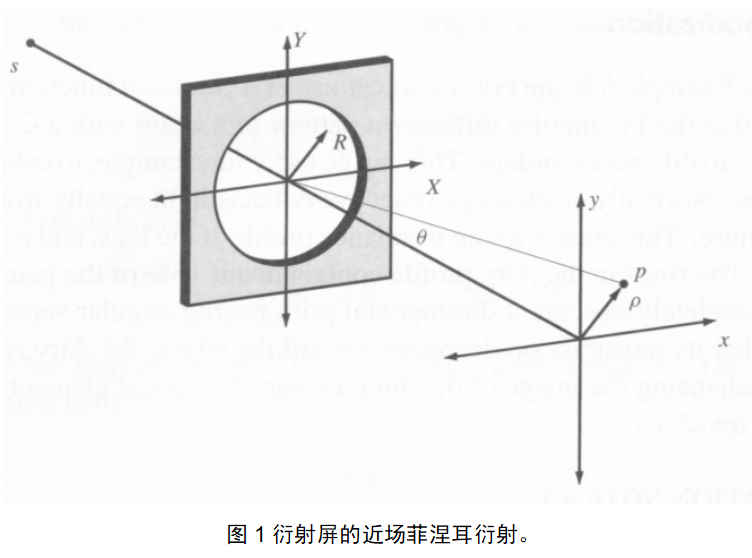
入射光波通过衍射屏(如图1),在衍射屏前方的任一点的波场,是该屏上各点产生的子波在该点的叠加。
在菲涅耳衍射方程
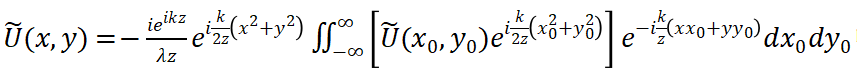
中被积函数指数项含有积分变量的二次式,使得衍射积分很难有解析解,对给定的衍射屏,一般采用数值求解。另一方面,人们提出了一种更为直观的求解方法,菲涅耳波带方法,通过该方法不需要复杂的数值计算即能获得菲涅耳衍射的许多主要特征。
菲涅耳衍射的数值求解
菲涅耳衍射满足衍射积分方程,当传输距离增大时,菲涅尔衍射转化为夫琅禾费衍射。转化条件通过菲涅耳数(Fresnel number)描述,假设衍射屏尺度为a,菲涅耳数
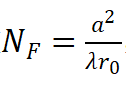
当NF《1时,衍射采用为夫琅禾费衍射描述;当时,必须采用菲涅耳衍射计算。通过数值计算菲涅耳衍射积分方程,展现光束衍射的演化过程。
菲涅尔衍射演化的数值计算

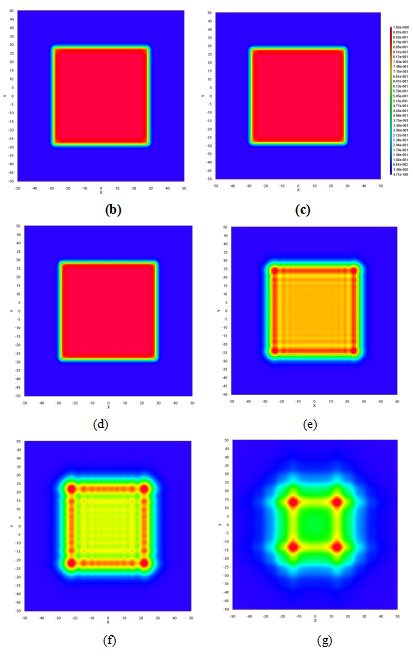
结论
在本篇文章中,讲解了菲涅耳衍射及其数值求解,、并在OAS中进行了菲涅尔衍射演化的数值计算模拟。